AlphaQubit tackles one of quantum computing’s biggest challenges

Quantum computers have the potential to revolutionize drug discovery, material design and fundamental physics — that is, if we can get them to work reliably.
Certain problems, which would take a conventional computer billions of years to solve, would take a quantum computer just hours. However, these new processors are more prone to noise than conventional ones. If we want to make quantum computers more reliable, especially at scale, we need to accurately identify and correct these errors.
In a paper published today in Nature, we introduce AlphaQubit, an AI-based decoder that identifies quantum computing errors with state-of-the-art accuracy. This collaborative work brought together Google DeepMind’s machine learning knowledge and Google Quantum AI’s error correction expertise to accelerate progress on building a reliable quantum computer.
Accurately identifying errors is a critical step towards making quantum computers capable of performing long computations at scale, opening the doors to scientific breakthroughs and many new areas of discovery.

Correcting quantum computing errors
Quantum computers harness the unique properties of matter at the smallest scales, such as superposition and entanglement, to solve certain types of complex problems in far fewer steps than classical computers. The technology relies on qubits, or quantum bits, which can sift through vast sets of possibilities using quantum interference to find an answer.
The natural quantum state of a qubit is fragile and can be disrupted by various factors: microscopic defects in hardware, heat, vibration, electromagnetic interference and even cosmic rays (which are everywhere).
Quantum error correction offers a way forward by using redundancy: grouping multiple qubits into a single logical qubit, and regularly performing consistency checks on it. The decoder preserves quantum information by using these consistency checks to identify errors in the logical qubit, so they can be corrected.
Here, we illustrate how nine physical qubits (small gray circles) in a qubit grid of side length 3 (code distance) form a logical qubit. At each step, 8 more qubits perform consistency checks (square and semicircle areas, blue and magenta when failing and gray otherwise) at each time step which inform the neural network decoder (AlphaQubit). At the end of the experiment, AlphaQubit determines what errors occurred.
Creating a neural-network contender for decoding
AlphaQubit is a neural-network based decoder drawing on Transformers, a deep learning architecture developed at Google that underpins many of today’s large language models. Using the consistency checks as an input, its task is to correctly predict whether the logical qubit — when measured at the end of the experiment — has flipped from how it was prepared.
We began by training our model to decode the data from a set of 49 qubits inside a Sycamore quantum processor, the central computational unit of the quantum computer. To teach AlphaQubit the general decoding problem, we used a quantum simulator to generate hundreds of millions of examples across a variety of settings and error levels. Then we finetuned AlphaQubit for a specific decoding task by giving it thousands of experimental samples from a particular Sycamore processor.
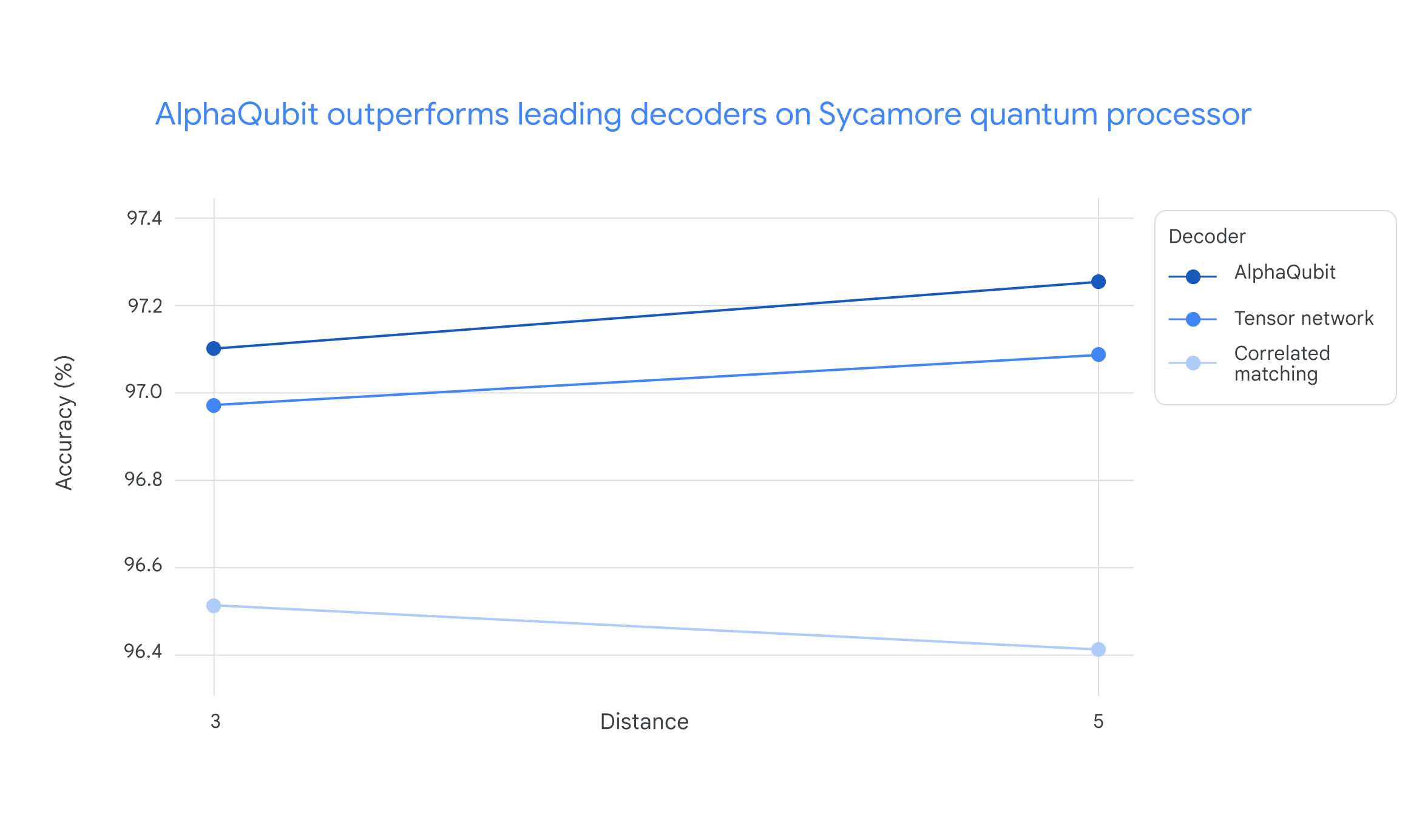
When tested on new Sycamore data, AlphaQubit set a new standard for accuracy when compared with the previous leading decoders. In the largest Sycamore experiments, AlphaQubit makes 6% fewer errors than tensor network methods, which are highly accurate but impractically slow. AlphaQubit also makes 30% fewer errors than correlated matching, an accurate decoder that is fast enough to scale.
Decoding accuracies for small and large Sycamore experiments (distance 3 = 17 physical qubits, and distance 5 = 49 physical qubits). AlphaQubit is more accurate than the tensor network (TN, a method that is not expected to scale at large experiments) and correlated matching (an accurate decoder with the speed to scale).
Scaling AlphaQubit for future systems
We expect quantum computers to advance beyond what’s available today. To see how AlphaQubit would adapt to larger devices with lower error levels, we trained it using data from simulated quantum systems of up to 241 qubits, as this exceeded what was available on the Sycamore platform.
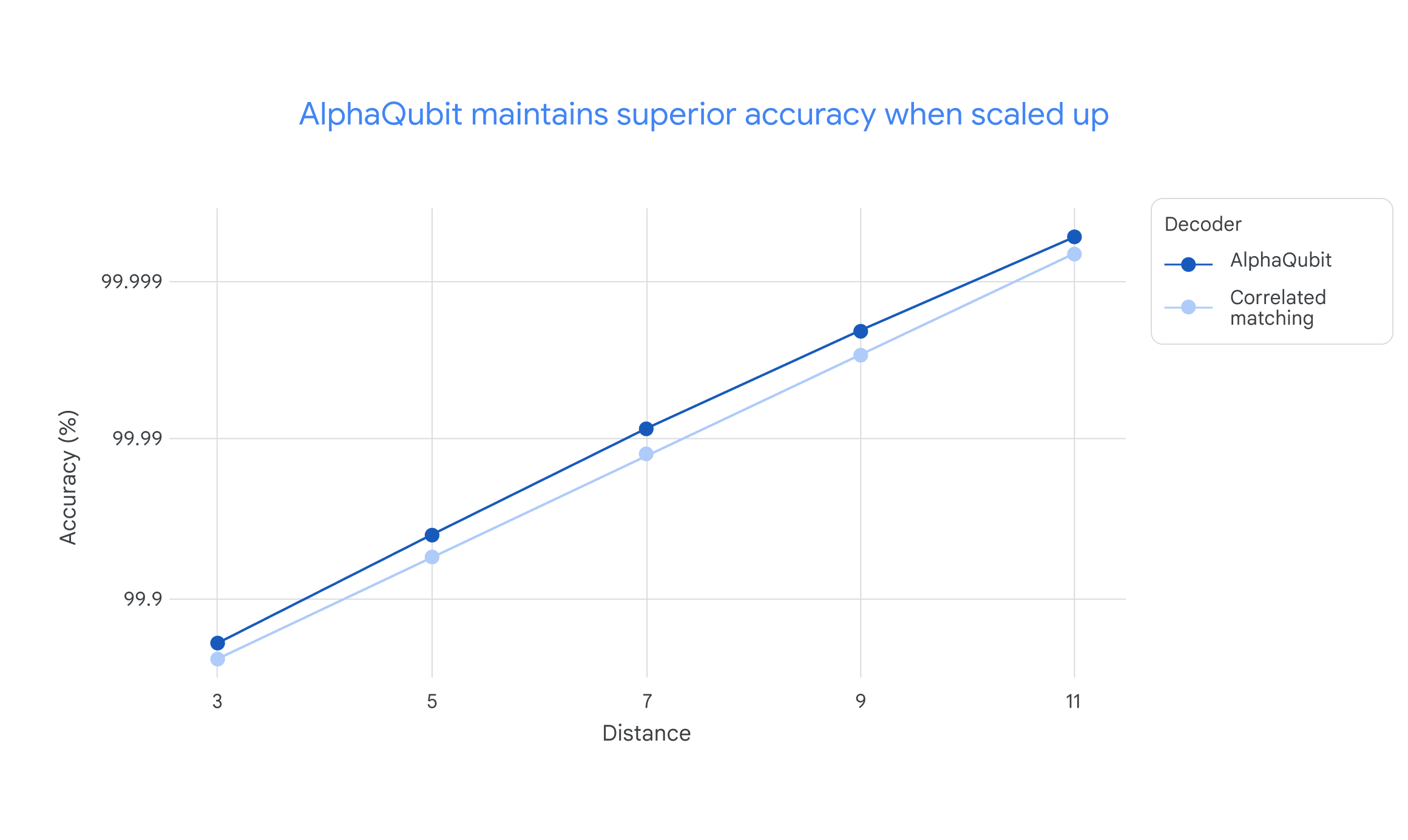
Again, AlphaQubit outperformed leading algorithmic decoders, suggesting it will also work on mid-sized quantum devices in the future.
Decoding accuracies for different scaling/simulated experiments, from distance 3 (17 qubits) to distance 11 (241 qubits). The Tensor Network decoder does not appear in this graph, as it is too slow to run at large distances. The accuracy of the other two decoders increases when increasing distance (that is, when using more physical qubits). At each distance, AlphaQubit is more accurate than correlated matching.
Our system also demonstrated advanced features like the ability to accept and report confidence levels on inputs and outputs. These information-rich interfaces can help further improve the performance of the quantum processor.
And when we trained AlphaQubit on samples that included up to 25 rounds of error correction, it maintained good performance on simulated experiments of up to 100,000 rounds, showing its ability to generalize to scenarios beyond its training data.
Moving towards practical quantum computing
AlphaQubit represents a major milestone in using machine learning for quantum error correction. But we still face significant challenges involving speed and scalability.
For example, each consistency check in a fast superconducting quantum processor is measured a million times every second. While AlphaQubit is great at accurately identifying errors, it’s still too slow to correct errors in a superconducting processor in real time. As quantum computing grows toward the potentially millions of qubits needed for commercially relevant applications, we’ll also need to find more data-efficient ways of training AI-based decoders.
Our teams are combining pioneering advances in machine learning and quantum error correction to overcome these challenges — and pave the way for reliable quantum computers that can tackle some of the world’s most complex problems.